虚構世界はなぜ必要か？SFアニメ「超」考察
第11回　量子論的な多宇宙感覚/『涼宮ハルヒの消失』『ゼーガペイン』『シュタインズゲート』(1)

　

　
　

フィクションとしての世界観と、それを揺るがす科学

科学は、技術やそれを用いた製品と結びつくことで私たちの生活に影響を与えます。それは私たちの生きる条件そのものを変えてしまいます。スマホを当然のように持ち歩く人にとって、そもそも電話がなかった時代に人々がどのように遠方の人と連絡を取り合っていたのかを想像するのも難しいのではないでしょうか。

しかしそれだけではなく、科学は世界の描像、あるいは世界観にも大きく影響を与えるでしょう。私たちは、自分の目で見たわけでもなく、自分でデータをとって計算したり検証したりしてみたわけでもないのに、我々の立つ大地は実は球形で、宇宙空間に浮かんでいて、空に見えているあの太陽の周りを回っているということを常識として共有しています。これはガリレオや二ユートンなど、17世紀の科学革命によってもたらされた世界観です。このような認識は物理学によって得られたものですが、私たちは必ずしも、物理学的な手続きを通してこの世界観を受け入れているわけではないでしょう。中世の人々が、空はドーム状で、世界の果てでは海の水が滝のように世界の外へこぼれ落ちていくという世界の像を自然に受け入れていたのと同じようなやり方で、つまり、教育や、メディアからの情報、映像、社会のなかでの人とのつき合いなどを通じて、共有された常識としてそれを受け入れていると言えます。

物の落下は、ニュートンが万有引力の法則として数学的に記述した式によって説明できます。我々もまた、物の落下が万有引力によるものだという世界観の下に生きています。あらゆる物体の間には質量と距離に応じた引力が働いているのだ、と。しかし、物理学者ではない一般の人々にとって、物の落下や運動は特に数学的にイメージされてはいないでしょう。アーチェリーで矢を放つ人は、物理学的にミサイルの弾道計算をする人とは、違ったやり方（イメージ）を用いて的を狙うでしょう。物理学は数学という言語で書かれていますが、世界観とは、イメージとして、直感として、感覚的に私たちのリアリティや（無意識的なものを含んだ）信念を下支えしているものだと言えます。

リアリティとは、何を現実として信じるのか、現実とはどのようであるか、という信念にかかわるもののことです。ブラックホールの存在は、一般相対性理論を数学的に厳密に解いてゆくことによって予測されました。つまり、仮に一般相対性理論が正しいとすると、必然的にこの宇宙にはブラックホールのような存在があることになるのです。しかしアインシュタインは、ブラックホールなどバカげているとしました。それは、彼にとっての現実への信念とは食い違っていたのです。残念ながらブラックホールは存在し、アインシュタインの信念（リアリティ）よりも数学の方が正しかったことになってしまいました。ブラックホールの存在は、アインシュタインの理論（一般相対性理論）の正しさを証明するとともに、アインシュタインの世界観（現実にかんする信念）の間違いを証明してしまいました。

ここで問題として取り上げたいのは、ハードサイエンスとしての物理学そのものではなく、物理学の発展によって、私たちの世界観がどのように影響され、揺るがされているのかということについてです。リアリティの基底としての世界観とは、私たちが「何を現実として信じ得るのか（何をリアルと感じるのか）」を下支えしているフィクション（信念）の枠組みだ、と言えるでしょう。つまり私たちは、「現実」を信じるために、出来事に現実感を与える何かしらのフィクションを必要としているということです。しかしそれはあくまでフィクションとしての枠組みなので、より強く現実的なものの出現（ここでは、数学やブラックホールが観測されたこと）によって否定され、書き換えざるを得なくなることがあるのです。

ここではまず、フィクションとしての世界観について検討する前に、その準備として、私たちの世界観を揺るがすものとして、現代の物理学がこの宇宙をどのように描き出しているのか、ざっくりとではありますが、概要を確認しておきましょう（今回は作品について触れるところまでは行きません）。
　

二重スリットの実験/粒子、波、量子の違い

地動説が17世紀のヨーロッパの人々の常識を揺るがせたのと同様に、現代の物理学もまた、私たちの常識とは大きく異なる世界の描像を示しています。相対性理論や、量子力学の体系の完成から約100年経過した現在でも、それらはまだ私たちの常識とうまく折り合いがつきません。相対性理論については以前触れています（第8回「相対性理論的な感情」）が、今回は量子力学について、基本的な部分を確認してみたいと思います。

まず、量子力学の説明といえば定番の「二重スリットの実験」について、ここではその数学的な意味をみてみたいと思います。粒子、波、量子についての数学的な記述が、それぞれどのように違っているのかをみます。量子が、粒子と波の両方の性質を併せ持つという時に、それが数学としてどう表現されるのか。数学といっても身構えるほと難しいものではありません。イメージとして考えるよりも、数学的に示す方がその違いがわかりやすいと考えます。

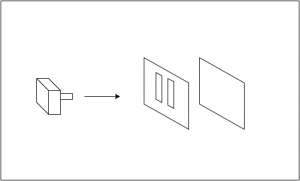
二重スリットの実験とは何でしょうか。まず、粒子、波、量子を発射する装置が一方にあるとします。そして、装置から発射されたものを受け止め、発射されたものがどこに当たったのかを記録する記録板があるとします。この板は、そこに当たった粒子、波、量子を吸収して、跳ね返すことがないとします。さらに、発射装置と記録板の間に、発射物を遮る壁を置き、この壁には二つの細い隙間（穴）が空いているとします（図1）。そして、この実験で問題となるのが「確率」であることを頭に置いてください。
　

　
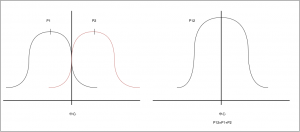
　まず粒子について。例えばマシンガンを壁に向けて撃ちまくるとイメージします。この時、記録板に記録される当たった弾（粒子）の数の確率分布はどうなるでしょうか（1万発の弾を撃ち、ある区画に100発当たっていたとすると、その区画に弾が当たる確率は1/100ということになります）。最も多くの弾が集中する（最も確率が高い）のは、二つの隙間の間の中心部分で、そこから離れるにしたがって着弾数は減ることになります。右側の隙間だけ空いていて左が塞がれている場合は右の隙間を中心とした同様の分布で、左側だけの場合も左の隙間を中心とした分布となります。つまり、右の隙間を通って着弾する確率の分布をP₁、左の隙間を通って着弾する確率の分布をP₂とすると、二つの隙間が空いている場合の確率は単純にP₁＋P₂になります（グラフ1）。
　 　
　次に波です。二重スリットの装置を水の中に置き、水面にさざ波をたてるイメージです。粒子の場合は当たった粒子（弾）の数の確率Pが問題でしたが、波の場合では確率は波の強さとしてあらわせます。波は空間に遍在しているので粒子のように1粒、2粒と数えられません。しかし、波に葉っぱを浮かべた場合、その葉っぱの行く先の確率は、波の強度に比例することになるので、強度を確率と考えてよいのです。波の強度Iは、波の高さhを2乗することによって得られます。波は三角関数によって表現され、三角関数のグラフはプラスとマイナス両方の値をとりますが、強度がマイナスでは都合が悪いので2乗してそろえることになります（グラフ2）。
　 　
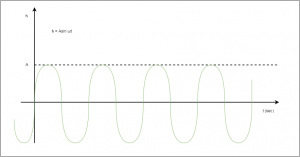
（波の強さとは波のエネルギーであり、エネルギーは速度の2乗に比例します。高さhを時間で微分すると速度になるので、高さの2乗が強度＝エネルギーと関係することは合理的です。）

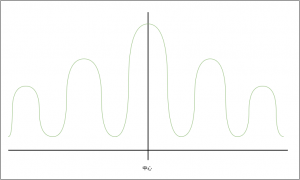
波の場合、確率＝強度の分布は、単純にI₁₂＝I₁＋I₂とはなりません。波は、隙間を通り抜けると左右に回り込んで折れる「回折」という現象を起こします。二つの隙間により波は二つに分岐するのです。さらに、二つの波が重なると「干渉」が起こります。山と山が合わさると約2倍の高さになり、谷と谷が合わさると約2倍の落ち込みになり、山と谷とが合わさると相殺してほぼゼロになるのです。この「回折」と「干渉」により、二重のスリットを通り抜けた波の強度＝確率の分布は、粒子のように中心で最も確率が高く周縁に行くにしたがって低くなるのではなく、縞模様のようになります（グラフ3）。
　

　
　以上、粒子と波までは古典物理学によってカバーできます。ここから先が量子力学の領域となります。粒子の実験の時のマシンガンの弾と同様に、発射装置からは電子を一つずつ発射するとします。そして、十分に多くの電子を発射した後、記録板に当たった電子の分布をみると、波の実験の時とまったく同じ干渉を示す分布のパターンがみられるのです。ここで問題が発生します。波が干渉を起こすのは二つの隙間を同時に通り抜けることによって波が二つに分岐するからでした。しかし電子は、自分一人（1個）だけで勝手に干渉を起こしてしまうのです。

これは数学的にどう表現されるのでしょうか。粒子の場合は確率Pが問題でした。波の場合は、まず高さhがあり、それを2乗することで強度Iが得られ、それが確率とみなされました。量子（電子）の場合は、波の高さhに相当するものとして確率振幅φというものが出てきます。波の場合と同様に、この確率振幅φを2乗することによって確率が得られるのです。しかし、波の高さが経験として観測することができるのに対し、量子の確率振幅φは、経験できる形で観測することができません。なぜならば、確率振幅φは、虚数iを含む複素数として記述されるからです。虚数は、2乗しない限り、経験可能な世界には姿をあらわすことのない数なのです。

虚数iとは、2乗するとマイナスになる数のことです（i²＝－1）。プラスとプラスをかけても、マイナスとマイナスをかけても、どちらもプラスになるはずなので、2乗するとマイナスになる数はあり得ません。少なくとも、経験可能な世界のなかにはあり得ません。しかし、経験可能ではない潜在的な世界が存在し、そこには虚数iという数の存在が何かしらの作用をし、それが2乗されることによって経験可能なこの世界に浮上してくると考えることはできます。

確率振幅φは複素数です。複素数とは、実数＋虚数という組成として記述されるものです（φ＝a＋bi）。なので、確率振幅φを2乗するという時、それは「φ²＝（a＋bi）²＝a²＋2abi＋bi²」という式で表されます。複素数（φ＝a＋bi）は、x軸を実数部分、y軸を虚数部分としてグラフにあらわすことができます（グラフ4）。
　

　
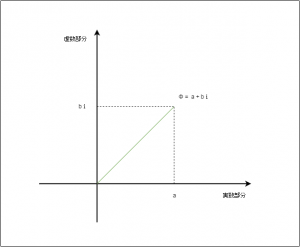
　量子（電子）の振る舞いの奇妙さは、まずは実数と虚数とが組み合わされた複素数という奇妙な存在に由来すると考えられます（とはいえ、複素数は電磁気学などにおいても必須の概念であり、量子力学だけが特別に複素数を用いるというわけではありません）。