因果推論

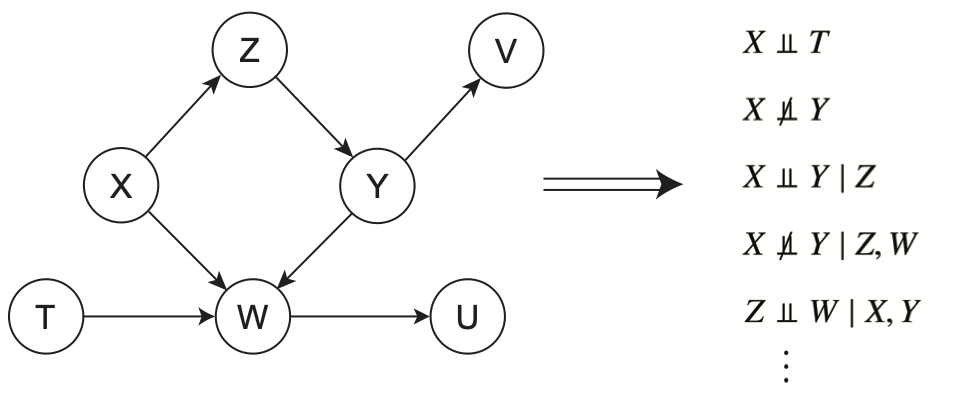
図1に示したのはDAGの一例であり，そこではいくつかの周辺独立性(あるいは従属性)と条件付き独立性(あるいは従属性)が示されている。このDAGの基盤となる構造的因果モデルは，以下のようにして与えられる。

\[ \begin{align*} X &:= \varepsilon_X \\ T &:= \varepsilon_T \\ Z &:= 1.25 \cdot X + \varepsilon_Z \\ Y &:= -0.75 \cdot Z + \varepsilon_Y \\ V &:= 0.50 \cdot Y + \varepsilon_U \\ W &:= 0.25 \cdot X + 0.50 \cdot Y + 0.75 \cdot T + \varepsilon_W \\ U &:= 1 \cdot W + \varepsilon_V \enspace , \end{align*} \] なお，上式においては\((\varepsilon_X, \varepsilon_T, \varepsilon_Z, \varepsilon_Y, \varepsilon_U, \varepsilon_W, \varepsilon_V) \sim \mathcal{N}(0, 1)\)となっている。

DAGの一例と，そこで示されているいくつかの周辺 / 条件付き独立性(あるいは従属性)

Question 1

図1のDAGを精査して，以下の問いに答えてほしい。

• \(X\)と\(T\)を\(d\)分離するのはどの変数か。
• \(Z\)と\(T\)の間に存在する，ブロックされていないパスをすべてリストアップしなさい。
• \(X\)と\(V\)をつなぐ一つひとつのパスについて，そのパスをブロックする変数をリストアップしなさい。すべてのパスをブロックするには，どのような変数のセットが最小のセットとなるだろうか。
• 最後に，このDAGに存在する周辺独立性と条件付き独立性をすべてリストアップしなさい。

Question 2

上記の問題に対する解答について検証するために，構造因果モデルから\(n = 2000\)のデータ点をシミュレーションで生成し，ピアソン相関検定と偏相関検定を用いて変数間の周辺 / 条件付き独立性について査定しよう。この問題に取り掛かる際には，以下のコードが助けになるだろう。

> library('bnlearn')
> set.seed(2)
> n <- 2000
> X <- rnorm(n, 0, 1)
> T <- rnorm(n, 0, 1)
> Z <- 1.25 * X + rnorm(n, 0, 1)
> # ...
>
> ci.test(X, T) # XとYの周辺独立性について検定する
> ci.test(X, T, Z) # Zを所与とした場合のXとYの条件付き独立性について検定する
> # ...

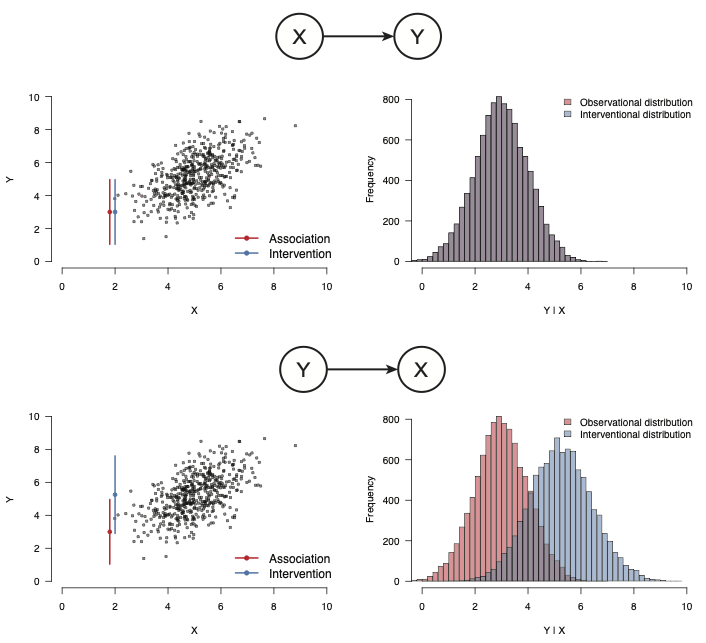
第12章では，下記の図2を検討した。これは，\(X \rightarrow Y\)のDAG(上段の2つのパネル)と，\(Y \rightarrow X\)のDAG(下段の2つのパネル)を対比させたものである。

（左上）\(X \rightarrow Y\)というDAGから生成されたデータ。赤い点と赤い直線は，「\(X\)がたまたま2となったことを所与とした場合の，\(Y\)の平均値と分布の95%区間」を表している。一方，青い点と青い直線は，「\(X\)を2と設定したことを所与とした場合の，前述と同様の数量」を表している。（右上）この場合，観測分布は介入分布と等しくなっている。（左下）DAG \(Y \rightarrow X\)というDAGから生成された全く同じデータ。（右下）この場合，観測分布と介入分布は異なっている。

Question 3

図2のデータは，以下の構造的因果モデルから，\(n = 500\)名分の観測値をシミュレーションに基づいて生成したものである。

\[ \begin{align*} X &:= 5 + \varepsilon_X \\ Y &:= 1.50 + 0.75 \cdot X + \varepsilon_Y \enspace , \end{align*} \] ここで\((\varepsilon_X, \varepsilon_Y) \sim \mathcal{N}(0, 1)\)とした。この知識をもとに，図2を再現してみよう。