ネットワーク構造についての記述的分析
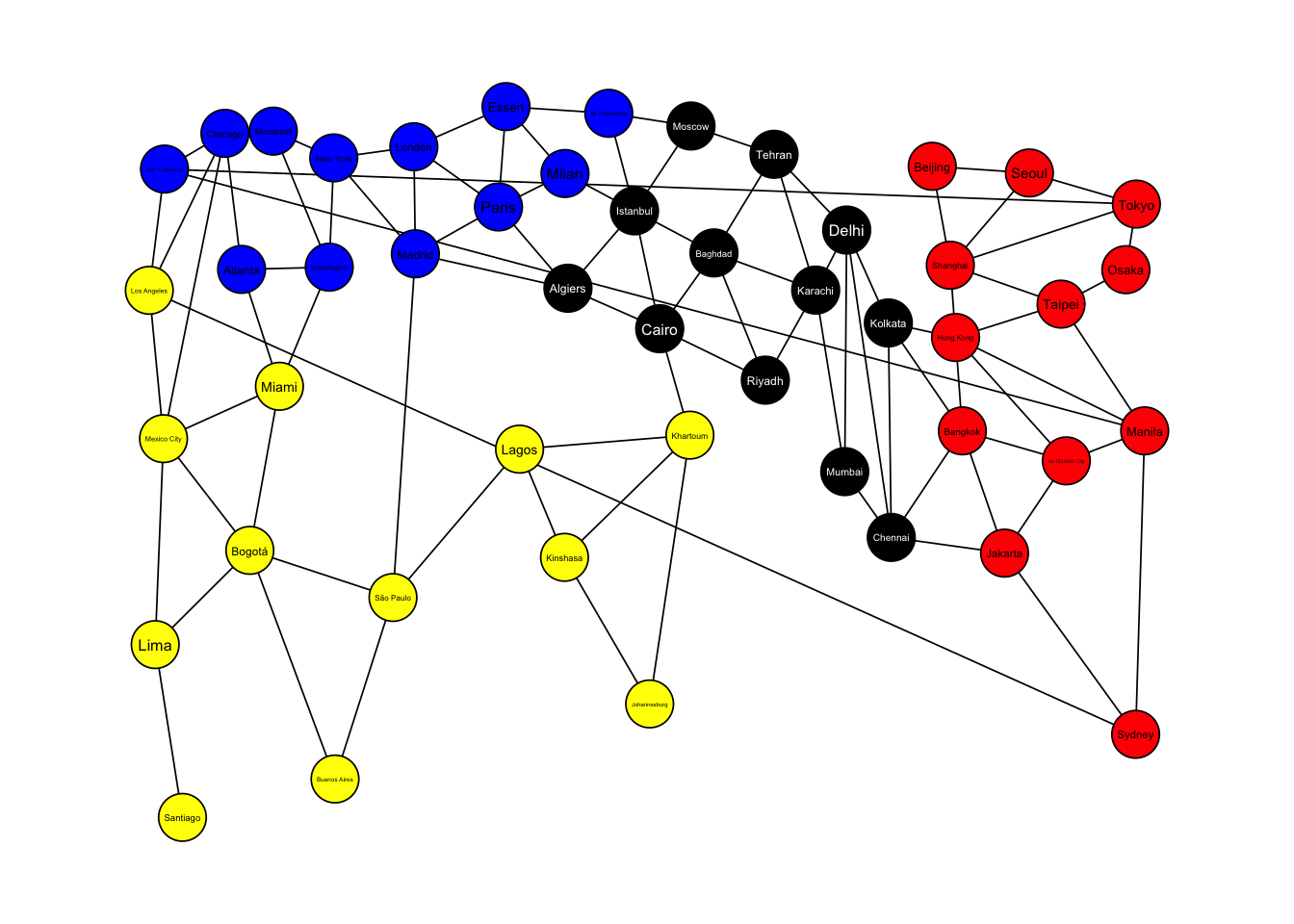
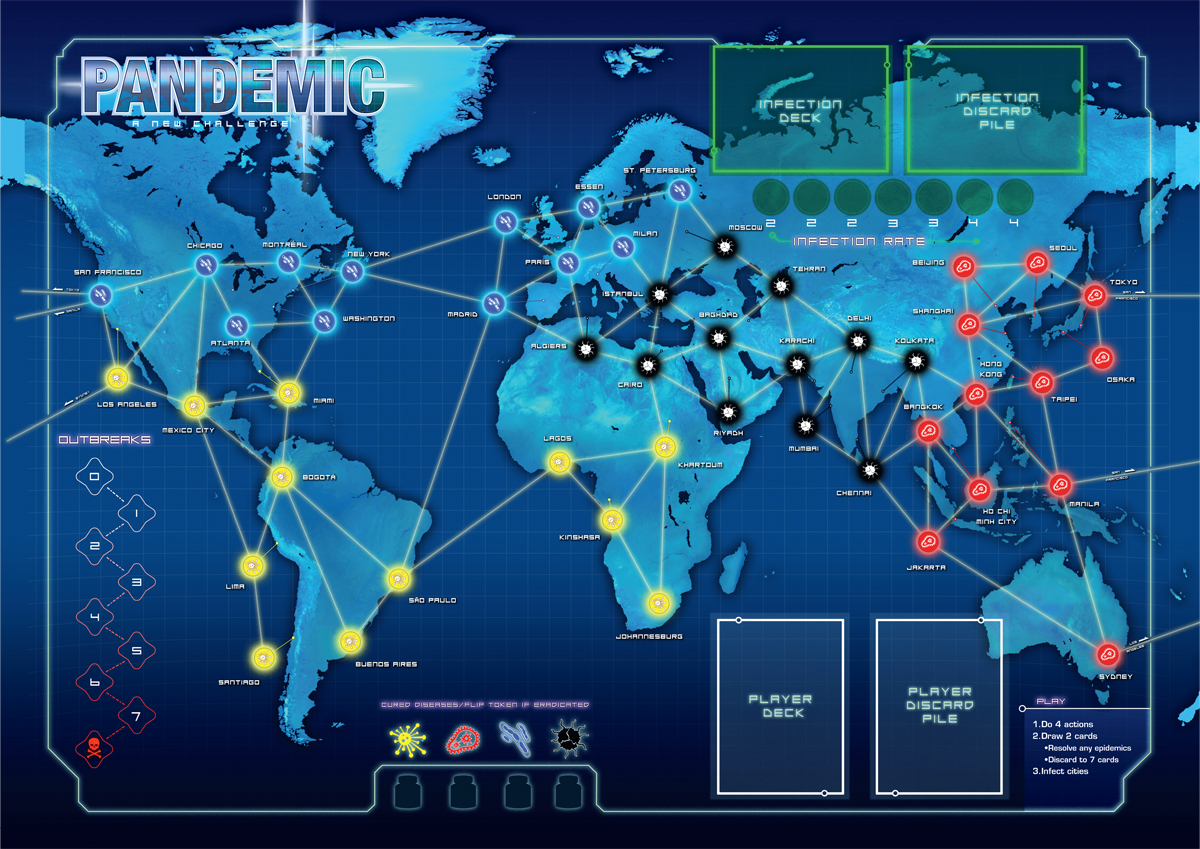
本書の著者のうち何名かは,「パンデミック」というボードゲームをプレイすることがたまにある。このゲームでは,4種類の凶悪なウィルスから世界を救うために協力することが目標となっている。このゲームでは,以下の画像のように,ボード自体がひとつのネットワークを表している。
青いウイルスは青い都市(ノード)で発生し,黄色いウイルスは黄色い都市で,黒いウイルスは黒い都市で,赤いウイルスは赤い都市でそれぞれ発生する。ひとつの都市でひとたびウイルスのアウトブレイクが起これば,エッジによって接続されている他の都市にもウイルスが拡散する可能性がある。だが幸いなことに,プレイヤーたちはウイルス拡散を止めるためのツールをいくつか持っている。たとえば,ひとつの都市を隔離して,当該のノードをネットワークからうまく取り除くことができる。
Exercise 1
以下の問題に,上の画像を眺めるというやり方だけで答えてほしい。
- 台北(Taipei)の次数中心性 (degree-centrality) はいくらか。
- アルジェ(Algiers)とムンバイ(Mumbai)間の最短パス長はいくらか。また,それと同じ長さのパスは何本あるか。
- すべてのノードペア間をつなぐ最短パスのうち,ブエノスアイレス(Buenos Aires)を経由するものはいくつあるか。
幸運なことに,上記のネットワーク構造を符号化するという重労働はすでになされており,オンラインで公開されている。
以下のコードを用いれば,このネットワークをRに読み込むことができる。
# ネットワークを読み込む:
library(igraph)
Graph <- read_graph("http://files.indicatrix.org/pandemic.graphml",
format = "graphml")
# エッジリストを取り出す
Edgelist <- get.adjacency(Graph)
# ラベルを読む
Labels <- V(Graph)$label
# レイアウト
Layout <- cbind(x = V(Graph)$x,
y = V(Graph)$y)
# カラー
Color <- c(
rep("blue",12),
rep("black",12),
rep("red",12),
rep("yellow",12)
)
# プロット
library("qgraph")
qgraph(Edgelist, labels = Labels,
color = Color, layout = Layout,
directed = FALSE,
vsize = 4, esize = 1, edge.color = "black")
続けて,各ノードがネットワーク内でどの程度重要であるか,つまり中心的であるかを分析できる。
いずれのノードが中心的であるかを分析するには,qgraphパッケージのcentrality関数を用いればよい。このことについては,第4章で詳しく学ぶことになる。
Centrality <- centrality(Graph, all.shortest.paths = TRUE)
ノード強度 (node strength)(次数とも呼ばれる)は,あるノードに接続されているエッジの重みを合計したものである。マイアミ(Miami)のノード強度は,以下の通りである。
Miami <- which(Labels == "Miami")
Centrality$OutDegree[Miami]
近接性(closeness)は,以下のように,ネットワークの中で2つのノードがどの程度「近い (close)」かを計算したものである。
Centrality$Closeness[Miami]
最後に,媒介性(betweenness)であるが,これは以下のように,「あるひとつのノードが,その他のノード同士を結ぶ最も効率的な(つまり,最短の)パス上にどの程度の頻度で出現するか」を計算したものである。
Centrality$Betweenness[Miami]
Exercise 2
バンコク(Bangkok)とアトランタ(Atlanta)という2都市の中心性を比較しよう。
Exercise 3
次数,近接性,媒介性のそれぞれについて,最も中心的なノードと最も中心的でないノードをリスト化しよう。なお,複数のノードが並んで中心的であった場合には,それらをすべてリスト化すること。
Exercise 4
「ラゴス (Lagos)」というノードの局所クラスタリング係数はいくらだろうか。Rを用いずに計算する方法を示してほしい。なお,計算の際には,もとのパンデミック・ボードを用いること。
Exercise 5
このネットワークのスモールワールド指標を計算しなさい。このネットワークは,スモールワールドネットワークといえるだろうか。なぜそういえるのか,あるいはいえないのかを,短い文章で説明してほしい。なお,qgraphパッケージのsmallworldIndex関数(詳細については,第3章の本文参照してほしい)を計算に用いても構わない。
以下のようにすれば,赤いウイルスが蔓延したすべての都市について次数を精査することができる。
Red <- which(Color == "red")
Centrality$OutDegree[Red]
[1] 2 3 4 5 6 4 2 5 4 5 4 3
Exercise 6
ウイルスごと(色ごと)に,次数,近接性,媒介性の平均値を計算しよう。どのウイルスが最も危険だといえるだろうか。