Data <- read.csv("stormofswords.csv")qgraphによるネットワークの構築と描画
ネットワークの可視化
ここの練習問題では,シリーズ本氷と炎の歌(A Song of Ice and Fire)の重みつき社会ネットワークを分析する。 この物語は,有名なテレビドラマシリーズゲーム・オブ・スローンズ (Game of Thrones)の原作となっている。このネットワークは,「数学の地平」誌(Math Horizon Magazine)上で公開されたものであり,テレビシリーズでいう第3,4シーズンにあたる,第三巻「剣嵐の大地 (A Storm of Swords)」を元にしたものである。データも含めてより詳しくはオンライン資料を参照のこと。公開されているネットワークは以下の通りである。
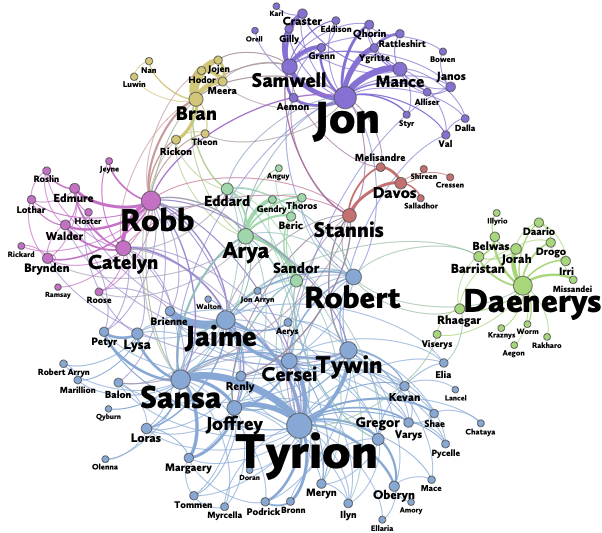
Exercise 1
このネットワークが何を表しているのかを理解するために,Network of ThronesのWebサイト上で公開されている記事をざっと見てみよう。ノードとエッジは,それぞれ何を表しているだろうか。
以下のようにすれば,オンラインで公開されているデータをRに読み込むことができる(データファイルは,こちらから入手できる)。
Exercise 2
RStudioでView関数を用い,データを眺めてみよう。この行列は,ひとつのネットワークを符号化したものである。どのようにして符号化されているかわかるだろうか。行は何を表し,列は何を表しているだろうか。
この構造は,ネットワークを符号化するエッジリスト (edgelist)として知られており,qgraphの入力として以下のように用いることもできる。
library("qgraph")
qgraph(Data, directed = FALSE)Exercise 3
隣接行列や重み行列を入力として無向グラフをプロットする際には,通常はdirected引数を指定する必要がない。しかし,今回のようにエッジリストを用いる場合には,directed引数を指定しなければならない。なぜそうなるのかを説明しなさい。
今度は,以下のデータセットを読み込もう。これもこちらから入手できる。
Data2 <- read.csv("stormofswords_wmat.csv")このデータセットは上記の同一のネットワークを表したものだが,表現形式が異なっている。この表現は重み行列(weights matrix)といわれている。
Exercise 4
View(Data2)を実行し,この新しいデータセットを精査してみよう。重み行列がどのようにしてネットワークを符号化しているかわかるだろうか。また,Data2を入力として,qgraph()を実行してみよう。上記と同一のネットワークは得られるだろうか。directed引数は,今回も必要だっただろうか。
プロットされたネットワーク図は,円形レイアウトを用いて描画されている。しかし,今回のようにノードが多いネットワークの場合,この円形レイアウトでは解釈や読み取りが困難となってしまう。さらに,正の値のエッジを表示する際に,緑ではない別の色で表示したいということもあるだろう。また,ノードが非常に大きくなっているので,もっと小さくしたいということもあるだろう。そのような操作を実行すると,以下のようなネットワーク図が得られる。

Exercise 5
上記のプロットを自分でも作ってみよう。つまり,レイアウトをスプリングレイアウトに変更し,エッジの色をdarkblue に変え,ノードのサイズを3に変更しよう。qgraphのヘルプページを参照し(?qgraph),必要なコマンドを探してほしい。なお,あなたの手元のコンピュータでは,解答例とまた異なったスプリングレイアウトが出力される(つまり,ノードが異なった場所に配置される)かもしれない。
qgraphでは,ネットワークの解釈に必要な3つの引数を用いている。それはminimum,cut,maximumの3つである。これらの設定は自動的になされるが,引数 detrils = TRUE と指定すればその設定を表示できる。
Exercise 6
1つ前の問題において,qgraphではcutとmaximumにどういった値が割り振られていただろうか。なお,minimumはデフォルトとして常に0と設定されている。そのため,0と異なる値が手動で設定されていない限りは,details = TRUEとしても表示されない。
minimum引数を用いれば,重みの絶対値が特定の値を下回るエッジを隠すことができる(つまり,負のエッジも正のエッジとして処理される)。ただし,それらのエッジは視覚的に隠されているだけであり,以降の分析で除外されているわけではないことに注意してほしい(以降の分析で除外したい場合には,threshold引数を用いるとよい)。この引数は,密なグラフ(たとえば,相関ネットワーク)をプロットする際には便利だが,本書で推定するようなネットワークの場合には推奨されない。
Exercise 7
スプリングレイアウトを用いる際に, minimum 引数を 1,10, 20と変えていってみよう。ネットワークはどのように変容するだろうか。また,同じことを今度は threshold引数を用いてやってみよう。minimum を用いた際にはレイアウトが同一のままだったのに,thresholdを用いた場合にはレイアウトが変わってしまう理由はなぜか,説明できるだろうか。
qgprahにおいては,エッジの重みの絶対値がより強く(大きく)なるにつれて,エッジがより太くかつより高い彩度で描かれるようになる。また,大きなネットワークの場合は,太さや色のスケールを途中で変更する(スプリットする)ことが有用だろう。cut引数が用いられるのはこのためである。つまり,重みの絶対値がカットオフ値を下回るエッジであれば,最も細い線で描画され,色だけが変動するということになる。一方,重みの絶対値がカットオフ値を上回るエッジであれば,彩度が常に最大となり(色は,緑と赤がデフォルトである),エッジが強くなるにつれてより太く描かれるようになる。なお,cut = 0と設定すれば,こうした挙動を無効化することができる。そうした場合には,いかなる場合でも,すべてのエッジが色と太さの両面でスケールに沿って変化するようになる。なお,qgraphでは,20個以上のノードを含むネットワークの場合にはカットオフ値が自動的に設定されるようになっている。しかし,そうした挙動が特別に必要だということでもない限りは,cut = 0と設定することを推奨しておく。
Exercise 8
スプリングレイアウトを用いる際に,cut引数を50, 10, 1と変えていってみよう。ネットワークはどのように変容するだろうか。今度は,cut引数を0に設定してみよう。何が起こるだろうか。
エッジのスケーリングは,そのネットワークに含まれる最も強い絶対値を持ったエッジを基準に選択される。なぜならば,エッジの重みはネットワークごとに大きく異なってくるからだ。上記の社会ネットワークの場合,エッジの重みはキャラクター間の相互作用の回数に基づいて決まっている。つまり,「ブラン(Bran)」と「ホーダー(Hodor)」というキャラクターが最も頻繁に交流しており(96回),最も強いエッジの重みが96になっているというわけだ。しかし(偏)相関に基づくネットワークの場合は,最も強いエッジの重みが1を超えるということはあり得ない(そして通常は,1よりも弱いエッジが目立つものである)。ここで,maximum引数を用いれば,エッジの色と太さのスケーリングの基準となる「エッジの最大値」を上書きすることができる。そこで指定した値は,見えないエッジの重みとして処理され,そのネットワークではその値こそが最大のエッジの重みとして設定される。maximumをより大きくしていくと,「ネットワーク内に実在する最も強いエッジ」の代わりにmaximumで指定した値を基準にエッジがスケールするようになる。
Exercise 9
maximum 引数を200に設定してみよう。何が起こるだろうか。今度は,maximumをデフォルトにいったん戻したうえで,10に設定し直してみよう。maximum = 200としたときにはネットワークが変容したのにmaximum = 10としてもデフォルト値からネットワークが変容しないのはなぜか。
Exercise 10
(偏)相関をもととしたネットワークを描く際には,maximumをどのように設定しておくのがよいだろうか。
Exercise 11
qgraphを用いて,このネットワーク構造についての中心性プロットを描画してほしい。プロットには強度,近接性,媒介性を必ず含め,z値は報告しないこと。ヒント:まずは,ネットワーク構造を個別のオブジェクトに保存しておく必要がある。