# Read data into R:
data <- read.csv("NA_2020_data.csv")ペアワイズ・マルコフ確率場
https://osf.io/45n6d/からファイル NA_2020_data.csv をダウンロードし,R に読み込もう。
これは,アムステルダム大学で2020年のネットワーク分析の講義で収集したデータセットである。以下のようにすれば,第6章の本文でも用いられていた変数を選択することができる。
# 含まれる変数名のリスト
include <- c(
"Q10", # 規則正しい睡眠パターンを維持しようと努めている
"Q13", # 自分の現在の睡眠行動について心配がある
"Q14", # 睡眠(不足) のせいで日常生活の機能に支障が出ている
"Q68", # 身体的な健康について満足している
"Q70", # 将来について楽観視している
"Q75", # とても幸せである
"Q77", # よく孤独を感じる
"Q80" # 性生活について満足している
)
# Subset the data:
subData <- data[, include]以下のようにして,もっと中身がわかりやすいように変数名を変更しておこう。
names(subData) <- c(
"regular_sleep",
"worried_sleep",
"sleep_interfere",
"happy_health",
"optimistic_future",
"very_happy",
"feel_alone",
"happy_love_life"
)ここで,以下のようにpsychパッケージのpartial.r を用いれば,偏相関を計算することができる。
library("psych")
# 「幸福感」と「孤独感」の間の偏相関を計算する:
partial.r(subData,
x = c("very_happy", "feel_alone"),
y = c(
"regular_sleep",
"worried_sleep",
"sleep_interfere",
"happy_health",
"optimistic_future",
"happy_love_life"
)
)partial correlations
very_happy feel_alone
very_happy 1.00 -0.27
feel_alone -0.27 1.00Question 1
ノードfeel alone と happy healthについて,周辺相関と,その他すべての変数で条件づけたうえでの偏相関の両方を計算しよう。ヒント:それらの相関を計算する際には,データに欠損値が含まれていることをしっかり考慮しておくこと。
以下のように,Rのcov関数を用いれば,標本の分散共分散行列を計算できる(訳注:この関数で算出されるのは,\(n-1\)で割った場合の不偏分散共分散であり,標本分散共分散そのものではないことに注意してほしい)。
covMat <- cov(subData, use = "pairwise.complete.obs")
round(covMat, 2) regular_sleep worried_sleep sleep_interfere happy_health
regular_sleep 3.02 -0.40 -0.32 0.56
worried_sleep -0.40 3.36 2.42 -0.66
sleep_interfere -0.32 2.42 3.63 -0.67
happy_health 0.56 -0.66 -0.67 2.47
optimistic_future 0.39 -0.74 -0.61 1.09
very_happy 0.34 -0.70 -0.68 1.08
feel_alone 0.12 0.93 0.91 -0.29
happy_love_life 0.39 -0.46 -0.27 0.58
optimistic_future very_happy feel_alone happy_love_life
regular_sleep 0.39 0.34 0.12 0.39
worried_sleep -0.74 -0.70 0.93 -0.46
sleep_interfere -0.61 -0.68 0.91 -0.27
happy_health 1.09 1.08 -0.29 0.58
optimistic_future 2.76 1.52 -0.74 0.83
very_happy 1.52 2.32 -1.06 1.21
feel_alone -0.74 -1.06 3.07 -0.94
happy_love_life 0.83 1.21 -0.94 4.37続けて,以下のように分散共分散行列の逆行列をとる (invert)ということを実行したい。
\[ \pmb{K} = \pmb{S}^{-1}.\]
Rでは,以下のようにsolve関数を用いることで,逆行列をとることができる。
Kappa <- solve(covMat)
round(Kappa, 2) regular_sleep worried_sleep sleep_interfere happy_health
regular_sleep 0.35 0.03 0.00 -0.06
worried_sleep 0.03 0.60 -0.37 0.03
sleep_interfere 0.00 -0.37 0.54 0.04
happy_health -0.06 0.03 0.04 0.56
optimistic_future -0.02 0.05 -0.02 -0.11
very_happy -0.01 -0.01 0.03 -0.18
feel_alone -0.05 -0.06 -0.05 -0.06
happy_love_life -0.02 0.02 -0.03 -0.01
optimistic_future very_happy feel_alone happy_love_life
regular_sleep -0.02 -0.01 -0.05 -0.02
worried_sleep 0.05 -0.01 -0.06 0.02
sleep_interfere -0.02 0.03 -0.05 -0.03
happy_health -0.11 -0.18 -0.06 -0.01
optimistic_future 0.60 -0.32 0.01 0.00
very_happy -0.32 0.88 0.17 -0.12
feel_alone 0.01 0.17 0.43 0.05
happy_love_life 0.00 -0.12 0.05 0.28この精度行列(precision matrix) \(\pmb{K}\) (カッパ) を以下の要領で標準化すれば,偏相関係数(変数 \(i\) と \(j\) を,データセットに含まれるその他のすべての変数で条件づけたうえでの偏相関)行列 \(\pmb{P}\) を得ることができる。
\[ p_{ij} = \begin{cases} - \frac{\kappa_{ij}}{\sqrt{\kappa_{ii}}\sqrt{\kappa_{jj}}} &\mbox{if } i \not= j \\ 1 & \mbox{if } i = j \end{cases}. \]
very happy と feel aloneの偏相関については,以下のように標準化を行って計算できる。
i <- which(names(subData) == "very_happy")
j <- which(names(subData) == "feel_alone")
-1 * Kappa[i, j] / (sqrt(Kappa[i, i]) * sqrt(Kappa[j, j]))[1] -0.2710972この値を丸めれば,先ほどの問題で計算した偏相関と値がぴったり一致する。
Question 2
上記の式を用い,feel aloneと happy healthの偏相関を計算しなさい。そして,その計算結果を,partial.rを用いて計算した場合の偏相関と比較しなさい。
ここまでのやり方とはまた別に,以下のようにcov2corを用いれば,すべての偏相関をワンステップで計算することもできる。
pcors <- -1 * cov2cor(Kappa)
diag(pcors) <- 1
round(pcors, 2) regular_sleep worried_sleep sleep_interfere happy_health
regular_sleep 1.00 -0.07 -0.01 0.13
worried_sleep -0.07 1.00 0.65 -0.04
sleep_interfere -0.01 0.65 1.00 -0.08
happy_health 0.13 -0.04 -0.08 1.00
optimistic_future 0.03 -0.08 0.03 0.19
very_happy 0.02 0.01 -0.05 0.26
feel_alone 0.12 0.12 0.10 0.11
happy_love_life 0.08 -0.04 0.07 0.01
optimistic_future very_happy feel_alone happy_love_life
regular_sleep 0.03 0.02 0.12 0.08
worried_sleep -0.08 0.01 0.12 -0.04
sleep_interfere 0.03 -0.05 0.10 0.07
happy_health 0.19 0.26 0.11 0.01
optimistic_future 1.00 0.45 -0.02 0.00
very_happy 0.45 1.00 -0.27 0.24
feel_alone -0.02 -0.27 1.00 -0.14
happy_love_life 0.00 0.24 -0.14 1.00また,もっとシンプルに済ませる方法として,以下のようにbootnet パッケージを用いることもできる。
library("bootnet")
# ネットワークの推定
Network <- estimateNetwork(subData,
default = "pcor"
)
# 重み行列の表示
round(Network$graph, 2) rg_ wr_ sl_ hp_ op_ vr_ fl_ h__
rg_ 0.00 -0.07 -0.01 0.13 0.03 0.02 0.12 0.08
wr_ -0.07 0.00 0.65 -0.04 -0.09 0.02 0.11 -0.04
sl_ -0.01 0.65 0.00 -0.08 0.03 -0.05 0.10 0.07
hp_ 0.13 -0.04 -0.08 0.00 0.19 0.26 0.11 0.01
op_ 0.03 -0.09 0.03 0.19 0.00 0.45 -0.02 0.00
vr_ 0.02 0.02 -0.05 0.26 0.45 0.00 -0.27 0.24
fl_ 0.12 0.11 0.10 0.11 -0.02 -0.27 0.00 -0.14
h__ 0.08 -0.04 0.07 0.01 0.00 0.24 -0.14 0.00# ネットワークの描画 (色覚障害に配慮したテーマがデフォルト設定)
plot(Network, vsize = 15, layout = "circle")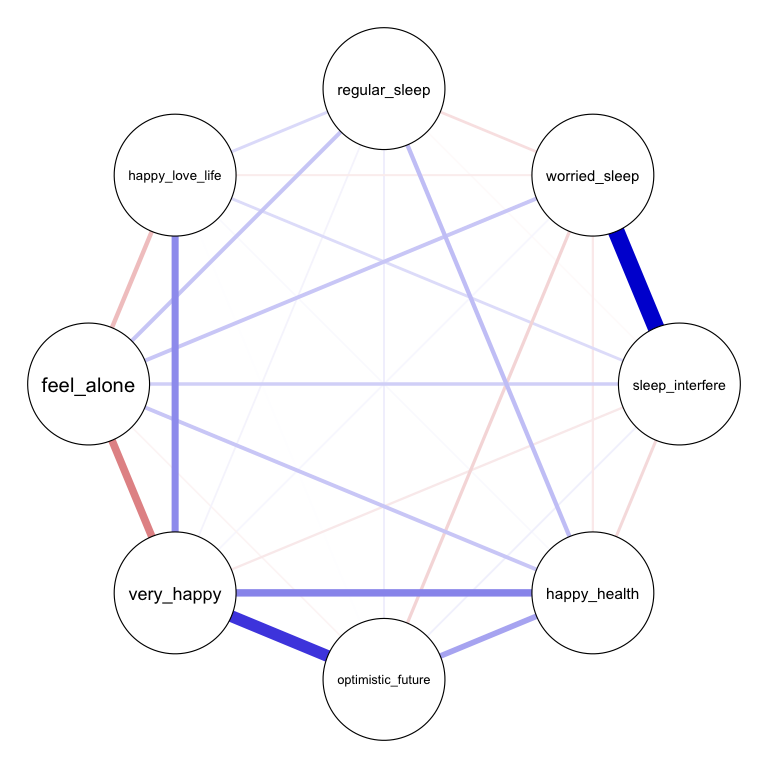
上の図は偏相関ネットワークであり,共分散行列を逆行列にしたうえで標準化することによって得られたものである。なお,引数corは,データの相関を取るための関数として用いることができる。
Question 3
bootnet パッケージを用いてネットワークを推定しよう。その際に,有意水準\(\alpha = 0.05\) に満たないエッジは除外する(閾値処理を施す)こと。この処理によって,何本のエッジが除外されるだろうか。結果として得られるネットワークを,円形レイアウトを用いてプロットしよう。
Question 4
psychonetrics パッケージでもガウシアン・グラフィカルモデルを推定してみよう。今回も,有意水準\(\alpha = 0.05\) に満たないエッジは除外すること(なお,psychonetricsパッケージでは,モデルを再度フィッティングすることができる。これを枝刈り (pruning)という。)。欠損値の処理には,オプションestimator = "FIML"を用いること。結果として得られるネットワークを,円形レイアウトを用いてプロットしよう。
Challenge question
第6章で紹介されているネットワーク(訳注:図6.1)は,psychonetrics パッケージを用いて推定されたものだが,枝刈りは施されていない。その代わりに,第6章では飽和推定を用いてエッジを非表示にしていた。このプロットを再現してみよう。