現実は変えられないという「現実主義」に抗するためにフィクションは意味をもち得るか、SFアニメで考える骨太フィクション論。
現実は変えられないという「現実主義」に抗するためにフィクションは意味をもち得るか、SFアニメで考える骨太フィクション論。
科学、技術の急速な発展をうけて、現実主義者は、フィクションは意味がないしくだらない、あるいは、無責任で害悪でさえあるという。それに対し、そのような態度こそがわたしたちの現実を堅く貧しくしているのだと反論することはできるのだろうか。名作SFアニメを題材に、フィクション、現実、技術について、深く検討する。本連載を大幅修正加筆し、2018年12月末刊行。
【ネット書店で見る】
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
古谷利裕 著
『虚構世界はなぜ必要か? SFアニメ「超」考察』
四六版判上製・304頁 本体価格2600円(税込2808円)
ISBN:978-4-326-85196-6 →[書誌情報]
相対性理論と技術
光格子時計と呼ばれる非常に精度の高い時計を用いることで、わずかな時間の流れの違いから標高差を測定することに成功したというニュースが最近ありました。一般相対性理論によると、重力が強い場所では時間がゆっくり進むことになるので、標高が低い場所の方が時間の流れが遅いのです。しかし地球上で生活する限りこの違いは無視してよいほどにわずかであり、従来の原子セシウム時計では違いを捉えることは困難でした。それが超高精度の光格子時計を用いることで、東京大学と理化学研究所との間にある15メートル程度の標高差を、誤差5センチ以内という精度で測定することができたということです。
絶対の基準であるはずの「時間」の流れる速度が異なるという事実は、常識的にはなかなか受け入れ難いものがあります。しかし、例えば上空を高速で移動しているGPS衛星と地上との時間の進み方の違いは、GPSを用いた地図上の位置と実際の位置との間に、1日につき10キロ以上のズレを生んでしまうほどに無視できないものだといいます(リサ・ランドール『ワープする宇宙』より)。そのズレを考慮して、GPS衛星内蔵の時計は、地上の時計に比べて毎秒100億分の4.45秒遅く進むように補正されているそうです(Wikipedia「時間の遅れ」の項より)。常識的、直観的には受け入れ難い相対性理論ですが、すでに我々が日常的に用いる技術のなかに組み込まれているのです。
光格子時計による標高差の計測は一般相対性理論に基づき、GPS衛星と地上との時間の進み方の違いは特殊相対性理論と一般相対性理論の両者に基づいて算出されるものですが、ここでは主に特殊相対性理論とフィクションとの関係を考えていきたいと思います。特殊相対性理論は主に運動と時空の関係を、一般相対性理論は主に重力と時空の関係をあらわしています。特殊相対性理論は、単独では重力の影響を無視できるような状況で有効です。
双子のパラドックス
特殊相対性理論は1905年にアインシュタインによって発表されました。その登場によって、「時間」は宇宙のどの場所でも均質に流れるという概念が崩れました。ニュートン力学では時間は絶対の基準であり、速度や加速度は基準である時間による微分によって、時間の関数としてあらわされました。しかし相対性理論以降、時間の流れはそれが属する慣性系によって異なることが分かり、基準としては、どの慣性系でも変わらない(ローレンツ変換に対して不変である)固有時という難しい概念が必要とされるようになります。
相対性理論によれば、あらゆる運動は相対的なものです。太陽を静止しているとみなせば、地球は太陽のまわりを公転していますが、その太陽もまた、この銀河のなかを移動しています。そしてこの銀河もまた、他の銀河に対して移動しているのです。あらゆる運動は相対的であり、これらの運動のすべての基準になる絶対的な座標(空間)はない、ということです。ここで慣性系とは、その運動が等速直線運動であるような系を指します。慣性系の運動体は、それを座標の基準とし、他の運動体に対して「静止している」とみなすことができます。相対性理論においては、等速直線運動と静止は等しいのです。それに対し、速度の変化をもつ運動体は加速度系と呼ばれます。加速度系に属するものには、慣性系に属するものよりも時間がゆっくりと流れることが分かっています(最短の世界線――等速運動=静止している状態――では固有時が最長になる)。
運動の相対性に関する「双子のパラドックス」と呼ばれるパラドックスがあります。AさんとBさんという双子がいるとします。Aさんは地球に留まり、Bさんは宇宙船に乗って非常に速い速度で地球から遠ざかるとします。特殊相対性理論によると、静止している系に対して、運動している系は時間がゆっくり進むことになります。Aさんから見た場合、BさんはAさんよりゆっくりと歳をとります。しかし相対論では、どのような運動も相対的ですから、Bさんを静止している(基準)とみなして、地球の方が宇宙船から遠ざかるように動いているとみることもできるのです。この場合、Bさんから見るとAさんの方がゆっくりと歳をとっているようにみえるのです。このどちらもが成り立つというのが相対性理論の帰結です。AさんとBさんとでは異なる時間の系を生きているのです。
ならば、Bさんが宇宙のどこかでターンして地球に戻り、Aさんと再会した場合、どちらが多くの歳月を経ていることになるのでしょうか。これが双子のパラドクスです。ここで、慣性系と加速度系の違いが効いてきます。地球にいるAさんは、ほぼ慣性系のなかにいると言えます。しかし宇宙船のBさんは、すくなくともターンするときに速度の変化を経ているはずです。そして、加速度系は慣性系に比べて時間の進みが遅くなります。つまり、再会時にはBさんの方が若いということになるのです。
ここで重要なのは、二人が出会う(再会する)ことがない限り、二人の距離が開きつづける限り、Aさんから見ればBさんの方が若く、Bさんから見ればAさんの方が若いというパラドクスの状態がそのまま成立しているということです。再会すること(再会のためにターンすること)によってはじめて、パラドクスの両立状態から、Bさんの方が若いという年齢のズレが生じる状態(ウラシマ効果)へと変化するのです。
(相対性理論の奇妙な効果はミュー粒子の地上到達という例からもうかがえます。太陽から発せられた宇宙線は大気圏で中間子やミュー粒子などに変化します。地上6キロメートルほどの高さの大気圏で生まれたミュー粒子は、光速の99.5パーセントという速さで地上に降ってきます。しかしミュー粒子の寿命はわずか2.2マイクロ秒程度なので、6~700メートル移動しただけで崩壊してしまう計算になります。ただし、その寿命はあくまで静止時のものです。光速に近い速さで運動しているミュー粒子において、時間は10分の1程度の遅さで流れます。よって、地上まで到達可能なのです。)
同時性について
αという出来事とβという出来事が同時に起きる、というのはどういうことなのでしょう。時間が絶対的な基準であるニュートン力学において、これは自明のことでしょう。同じ時刻に、別の場所で二つの出来事が起こった、ということです。しかし、特殊相対性理論を受け入れると、同時性という概念は自明ではなくなります。
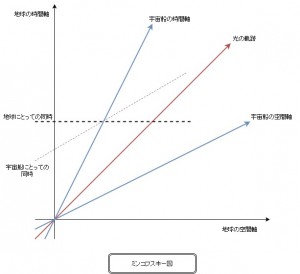
再びAさんとBさんに登場してもらいましょう。Aさんは地球にいます。Bさんは宇宙船に乗って光速の半分の速さで地球から遠ざかっているとします。この場合、AさんとBさんとは異なる慣性系に属することになります。二つの異なる慣性系の関係を一つの平面的な図に表す方法に、ミンコフスキー図があります。これは、チューリッヒ大学でアインシュタインを教えたこともあるアーマン・ミンコフスキーによって考案されたものです。
図を見てください。座標の縦軸にあたるものを、地球の時間軸とし、横軸にあたるものを地球の空間軸とします。ずっと地球にいるAさんは、原点から地球の時間軸上を上へ向かって移動していることになります。直交する縦軸と横軸に対して45度の角度で伸びている線は、原点の時刻に地球から発した光の軌跡をあらわします。つまり、光速で地球から離れてゆく運動です。
この時、光速の半分の速さで地球から離れてゆくBさんの時間軸は、地球の時間軸と光の軌跡との角度を二等分したところに引かれます。そして、Bさんの空間軸は、光の軌道と地球の空間軸の角度を二等分するところに引かれます。地球を静止しているとみなした場合、地球から光速の半分の速度で離れてゆくBさんの慣性系の時間軸と空間軸は、交わる角度が半分に縮むのです。
ニュートン力学において同時性とは、同じ時刻に起こったことでした。特殊相対性理論においても同様ですが、ここではその基準となる時刻が慣性系によって異なっているのです。ミンコフスキー図において「同じ時刻」は、空間軸と平行する線によって表現されます。図を見れば一目瞭然ですが、ここでは、慣性系A(地球)にとっての慣性系B(宇宙船)との同時と、慣性系B(宇宙船)にとっての慣性系A(地球)との同時が食い違ってしまうのです。つまり、Aにとっての現在と、Bにとっての現在は別の平面であることになります。